In November we posted an article on the Chem Soc Rev blog entitled Time to hook up the switches. The article was about a Chem Soc Rev Tutorial review by Ali Coskun, Michal Banaszak, R. Dean Astumian, J. Fraser Stoddart and Bartosz A. Grzybowski called ‘Great expectations: can artificial molecular machines deliver on their promise?’ Since then, there have been some interesting comments about the review posted by mol machines guy. I’ve copied these below along with a detailed response from Coskun et al.
What do you think? Join the discussion by posting your comments below.
mol machine guy says:
This is a rather confused Tutorial Review. The difference between molecular switches and more complex molecular machines, notably motors, has previously been discussed at length by Leigh’s group in their 2006 paper “Beyond Switches: Ratcheting a Particle Energetically Uphill with a Compartmentalized Molecular Machine” J. Am. Chem. Soc. 2006, 128, 4058-4073 (remarkably not cited in the Stoddart review). That paper included all the points about the need to avoid reciprocal motion (not, as incorrectly stated in this CSR review, “reversible” motion) and was further elaborated on in the 2007 review “Synthetic Molecular Motors and Mechanical Machines” Angew. Chem. Int. Ed. 2007, 46, 72-191.
Some of the statements in the CSR are just plain wrong. In the “Roadmap” (Fig 8 ) it states prominently that Artificial Molecular Switches “Cannot do Work!”. Not only can molecular switches do work, they have been measured doing so both collectively (e.g. ACS Nano, 2009, 3, 291–300) and at the single molecule level (Nature Nanotech. 2011, 6, 553-557). What switches cannot do is *progressively* perform work. That is, after performing one work cycle a switch cannot be reset to do more work without undoing the work it did previously (as discussed in the 2006 JACS and 2007 Angew Chem papers mentioned above). To do that requires a ratchet mechanism (as outlined in Fig 4 of the CSR, without use of the term “ratchet”).
Whilst it is probably progress that the authors now recognize (p3 of the CSR) that they have been claiming too much (again, see the earlier Leigh papers and also Chem. Soc. Rev., 2011, 40, 3656–3676 for gentle hints at this) in categorizing their molecular switches as “motor-molecules” in many previous papers, it might be better if they didn’t continue to confuse the issue by still claiming that palindromic bistable rotaxanes are somehow phenomenologically different to other molecular switches that they say are “ten a penny”. There are synthetic molecular machines that are not switches (the Feringa rotary motors, some DNA walkers and some of Leigh’s small-molecule walking molecules), but bistable rotaxanes are not amongst them.
Commentary Response
by
Ali Coskun, Michal Banaszak, Dean Astumian, Fraser Stoddart and Bartosz Grzybowski
Unfortunately, the authors of the commentary apparently seriously misunderstand both our Tutorial Review and several of the papers from Leigh’s group. The authors claim that the paper (J. Am. Chem. Soc. 2006, 128, 4058‒4073) entitled “Beyond Switches: Ratcheting a Particle Energetically Uphill with a Compartmentalized Molecular Machine” included all the points about the need to avoid reciprocal motion. In fact, that paper does not even contain the words reciprocal or non-reciprocal. The JACS paper correctly invokes “breaking” detailed balance (a corollary of microscopic reversibility) as the key to doing work with a molecular machine. This point has, of course, been made by many authors. The important question, which we address explicitly in our Tutorial Review, is HOW to circumvent detailed balance at the single molecule level.
The review article (Angew. Chem. Int. Ed. 2007, 46, 72‒191) entitled “Synthetic Molecular Motors and Mechanical Machines” does discuss reciprocal motion as a potential mechanism for directed transport of molecules (see Fig. 34 in that review). Fig. 34d of that paper involves a photochemical process which explicitly breaks (or more precisely circumvents) microscopic reversibility. Although the authors of that paper did not explain it clearly, Leigh and colleagues certainly must have realized that the thermally activated processes in the three-part, two-hinge molecule shown in their Fig. 34c would be constrained by microscopic reversibility, i.e., any individual molecule would undergo many non-reciprocal clockwise cycles every second. The molecule would also undergo many counter-clockwise non-reciprocal cycles every second. The average of the number of clockwise cycles would exactly equal the average of the number of counter-clockwise cycles irrespective of any asymmetry built into the molecule during its synthesis. This outcome is the essence of detailed balance or microscopic reversibility, and it is this microscopic reversibility that must be circumvented.
The authors of the commentary also criticize our claim that switches alone do not do work. Trivially, of course, the motion of any atom relative to another atom involves “doing” or “receiving” work since the process involves an object moving a certain distance in the presence of a force! Indeed, as the authors of the commentary point out, this trivially obvious fact can be experimentally measured when some of the atoms are attached to an AFM and a geometrical change is stimulated externally. What we mean (and we think it is very clearly stated in our review) is the performance of work in a cyclic process occurs when one form of free energy in the environment (e.g., chemical free energy) is converted into another form of free energy in the environment (e.g., mechanical free energy) and where the molecular machine cycle can continue.
For clarity let us consider the original “ratchet” mechanism, first termed electro-conformational coupling from the context in which it was proposed (Westerhoff et al., Proc. Natl. Acad. Sci. USA. 1986, 83, 4734‒4738; Astumian et al., Proc. Natl. Acad. Sci. USA. 1987, 84, 434‒438).
This scheme describes a transporter molecule which spans a bilayer membrane and facilitates the transport of an uncharged substance S across the membrane. The transporter has two conformations, A with the binding site for S facing to the left hand side of the membrane, where the chemical potential of S is μs,l, and B, with the binding site for S facing to the right hand side of the membrane, where the chemical potential of S is μs,r. By microscopic reversibility the product of the equilibrium constants must equal unity, K1K2K3K4 = 1, which can also be written K1K3 = (K2K4)-1.
Since there is some charge transfer in the conversion between the A and B forms, an electric field can serve as an external stimulus to switch the molecule from one form to another. Charge transfer in biomolecular transporter conformational changes is very common ― e.g., voltage gated (or switched) channels ― and can be very large, e.g., the equivalent of five or more elementary charges (zd = 5) moving across the membrane.
For any constant transmembrane potential difference, ψ ≠ 0, every transition between A and B, whether bound or not, involves the molecule doing work on or receiving work from the electric field. Nevertheless, microscopic reversibility assures that there is no net electrical work done on/received by the transporter in any cycle, irrespective of the value of Δμ = μs,l – μs,r . The situation is dramatically different when the membrane potential depends on time, either periodically (Westerhoff et al., Proc. Natl. Acad. Sci. USA. 1986, 83, 4734‒4738) or randomly (Astumian et al., Proc. Natl. Acad. Sci. USA. 1987, 84, 434‒438). The AC field can drive transport of a substrate against a small gradient (from low to high chemical potential) and a sufficiently large concentration gradient can do net work on the applied field (Derenyi and Astumian, Phys. Rev Lett., 1998, 80, 4602‒4605). A required asymmetry is assured by K1K3 ≠ 1 ; when K1K3 > 1 a time dependent ψ tends to drive transport of S from left to right, and vice versa when K1K3 < 1. The thermodynamic efficiency is optimized when the inter-conversion between A and B and between sA and Bs is very fast so that the energy input is nearly reversible.
Let us restate the necessary steps that need to be taken to realize a molecular machine: they are ―
(1) Design a molecule with a cycle of states, the completion of which in one direction accomplishes a desired task. Completion in the opposite direction undoes the task!
(2) Build in a switching function by which the relative stability of two states in the cycle can be controlled externally.
(3) Design an asymmetry such that switching kinetically favors one path, while reset favors the other.
(4) Operate the machine by externally switching/resetting. The molecule will proceed in a directed way cyclically, thereby accomplishing its appointed task, even if there is a small load tending to undo that task.
There is clearly a real lack of agreement in the literature as to what constitutes a molecular switch and what constitutes a molecular machine (or motor). While we can seek to bring more precision into the argument, we should ALL recognize that the excellent progress that is being made today in several different laboratories around the world finds its intellectual inspiration ― not to mention its technical basis ― from the early beginnings of the field.
We thank the authors of this commentary for their critical comments.
Comments Off on Can artificial molecular machines deliver on their promise? – a discussion
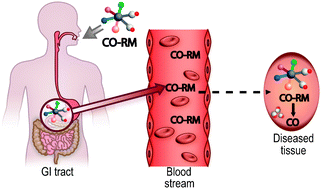Well, no. Last century a physician discovered that our bodies produce CO. Not only that, but CO levels are higher in sick people than healthy. This suggested that CO could actually be therapeutic and sparked interest from pharmaceutical chemists.
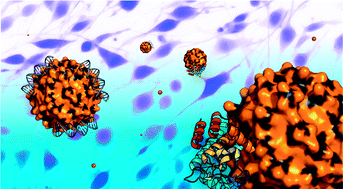Just as you would dress up to go to a 5 star restaurant, swapping your jeans and T-shirt for a suit jacket and tie, a nanoparticle’s coating needs to be tailored to suit the application. Nanoparticle ‘coats’ can be made from a variety of ‘fabrics’ which include small molecules that change the surface charge and therefore the cellular uptake properties. Polymer coatings can create ‘stealth’ nanoparticles, preventing serum protein adsorption thus increasing circulation times in the body, whilst other polymers act as gate keepers allowing drugs to escape from nanocages only when desired. If the coat is made from biomolecules, they can be selected so the resulting nanoparticle will actively target specific cancerous tumours.
