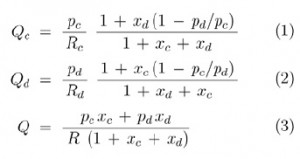Piotr M. Korczyk [1,2], Olgierd Cybulski [1], Sylwia Makulska [1] and Piotr Garstecki [1]
[1] Institute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland
[2] Institute of Fundamental Technological Research, PAS, Pawinskiego 5B, 02-106 Warsaw, Poland
Why is this useful?
Syringe pumps are known to generate fluctuation of rate of flow (1). In some applications the impact of these oscillations can be relevant. We demonstrate and characterize in detail a simple method for feeding fluids into microfluidic devices at a constant rate of flow. This simple experimental setup provides for more precise control and for better stability of the rate of flow than the commonly used syringe pumps.
What do I need?
- Source of pressurized gas
- Tubing for pressurised gas
- Pressure regulator
- Pressure transducer
- Container for pressurized liquid
- Polyethylene tubing
- Steel capillaries
- Tygon tubing
- Needles
How do I do it?
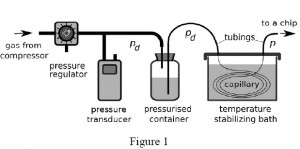
1. Connect pressure source with pressure regulator via tubing and then with the pressurized container filled with carried liquid (Fig. 1).
2. Place pressure transducer between the regulator and the container (Fig. 1).
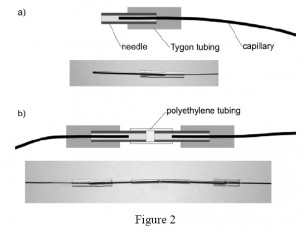
3. For connections between the polyethylene tubing and the steel capillaries use short sections of the Tygon tubing. In order to avoid obstruction of the terminus of the capillary by the elastic Tygon, first put a blunted needle all the way through the Tygon tubing. Then insert the terminus of the capillary into the needle, and partially withdraw the needle from the Tygon to let it squeeze around the capillary and seal the connection (Fig. 2).
4. Connect the end of the capillary with the pressurised container for liquid via a polyethylene tubing and the other end of the capillary with the chip (Fig. 1).
5. Place the resistive capillary into a temperature stabilizing bath of liquid (e.g. water) to avoid temperature fluctuations which can affect viscosity of the liquid guided through the capillary and its hydraulic resistance to flow (Fig. 1).
What else should I know?
Using the resistive capillaries for delivering stable rates of flow requires calibration of the hydraulic resistance of the capillary. First estimate the Reynolds number for the flow on the basis of the dimensions of the capillary and the range of required rates of flow. If the flow is laminar, the relation between the pressure P applied to the container with liquid and the rate of flow Q through the capillary is linear: P=RQ where R is the hydrodynamic resistance. In order to calibrate for R place the capillary in the bath and apply a known pressure to the container. Then evaluate the rate of flow by measuring the rate of change of mass on an analytical balance collecting the liquid flowing out from the capillary.
The ratio of P/Q yields R. Alternatively, for more precise calibration collect a number of values of Q for different values of P and fit a line: P = RQ to retrieve R.
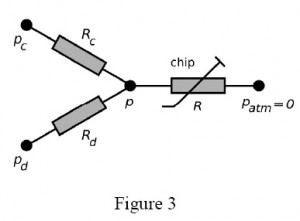
Figure 3 presents example of the equivalent electric circuit of the system that draws a continuous liquid (under pressure pc and a to-be-dispersed fluid (pd) from pressurized containers to form droplets on a microfluidic chip. The capillaries have hydrodynamic resistances Rc, Rd, the pressure at the droplet generator is p. The droplets flow through a channel of resistance R (varying, due to the generation and motion of droplets) up to the outlet (pressure 0, since all pressures are relative to the atmospheric pressure).
In general, having capillaries of known resistance (e.g. already calibrated for a desired liquid), one may easily calculate the rates of flow of the continuous phase (Qc) and of the droplet phase (Qd) from Ohm and Kirchhoff circuit laws:
where xc = R/Rc and xd = R/Rd.
It should be noted that although Qc and Qd are not mutually independent functions of respective pressures pc and pd, the cross-dependency becomes irrelevant for small values of xc and xd i.e. when the resistance of the capillaries is much larger than the resistance of the chip. Keeping Rc >> R and Rd >> R also minimized the variation of Qc and Qd in response to the variation of R. It is practical to to have pc and pd of similar magnitude, hence for a given range of rates of flow the user should tailor resistance of capillaries to meet the following condition: Rc / Rd ≈ Qd /Qc.
References
(1) R. Green and S.A. Vanapalli, Quick assessment of the stability of flow generated by a syringe pump in a microfluidic device, Chips & Tips (Lab on a Chip), 16 July 2009.
(2) P. Korczyk, O. Cybulski, S. Makulska, P. Garstecki, Effects of unsteadiness of the rates of flow on the dynamics of formation of droplets in microfluidic systems, Lab Chip, DOI:10.1039/C0LC00088D.